Speculative Ensemble: Fast Large Language Model Ensemble via Speculation
Published in Arixv, 2025
1. Introduction: The Need for Efficient Ensemble Inference
While ensemble methods combining multiple Large Language Models (LLMs) enhance prediction robustness and accuracy, their computational demands create significant deployment challenges. Traditional approaches requiring \(O(nT)\) operations for \(n\) models generating \(T\) tokens prove impractical for real-time applications due to linear scaling of latency with model count.
We present Speculative Ensemble (SE), a novel framework that synergizes speculative decoding with ensemble theory to achieve 1.11×–2.23× speedups over conventional ensembles while preserving output quality. Our key innovation lies in reimagining the proposal-verification paradigm to enable parallelized token generation while maintaining statistical equivalence to standard ensemble distributions.
2. Background: From Speculative Decoding to Ensemble Acceleration
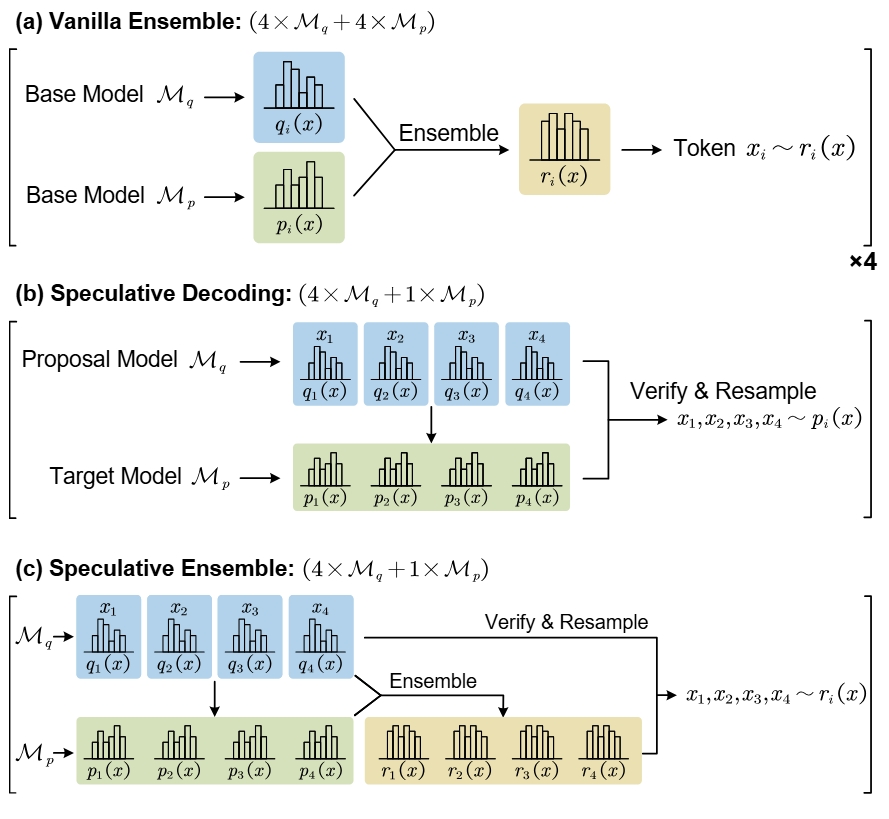
Figure 1. Comparison of (a) vanilla ensemble, (b) speculative decoding, and (c) speculative ensemble. In (b) and (c), each discrete blue block represents a probability calculated by one forward pass of \(\mathcal{M}_q\), while the continuous green block indicates the joint distribution requires only one forward pass of \(\mathcal{M}_p\).
2.1 Limitations of Vanilla Ensembles
Standard ensemble methods compute token distributions through weighted combinations:
\[ r_i(x) = \sum_{k=1}^n \lambda_k p_i^{(k)}(x) \]
This sequential process (Figure 1(a)) necessitates n×T model invocations, creating fundamental latency barriers.
2.2 Speculative Decoding Revisited
Speculative decoding (SD) accelerates autoregressive generation by leveraging two models:
- Proposal Model (\( \mathcal{M}_q \)): A lightweight model rapidly generates candidate tokens.
- Target Model (\( \mathcal{M}_p \)): A larger model verifies proposals in parallel.
For a proposal sequence \( x_{i+1}, \ldots, x_{i+\gamma} \sim \prod_{j=1}^\gamma q_{i+j}(x) \), the target model computes verification distributions \( p_{i+j}(x) \). Tokens are accepted if:
\[ u_j \leq \min\left(1, \frac{p_{i+j}(x)}{q_{i+j}(x)}\right), \quad u_j \sim \mathcal{U}(0,1) \]
Rejected tokens trigger resampling from \( \text{norm}(\max(0, p_{i+j} - q_{i+j})) \). This process is depicted in Figure 1(b).
3. Speculative Ensemble
3.1 A Two-fold Innovation
Speculative ensemble (SE) is based on the following two insights:
Ensemble Distribution as Verification Criterion
Speculative decoding (SD) allows not only sampling from the target model’s distribution, but also sampling from the ensemble distribution of the proposal model and target model. Adopted this, SE redefines the verification step of SD to sample from the ensemble distribution \( r_i(x) \) rather than a single target model, as illustrated in Figure 1(c). For a two-model ensemble:
\[ r_i(x) = \lambda q_i(x) + (1-\lambda) p_i(x) \]
The acceptance criterion becomes:
\[ u_j \leq \min\left(1, \frac{r_{i+j}(x)}{q_{i+j}(x)}\right) \]
Alternating Proposal Framework
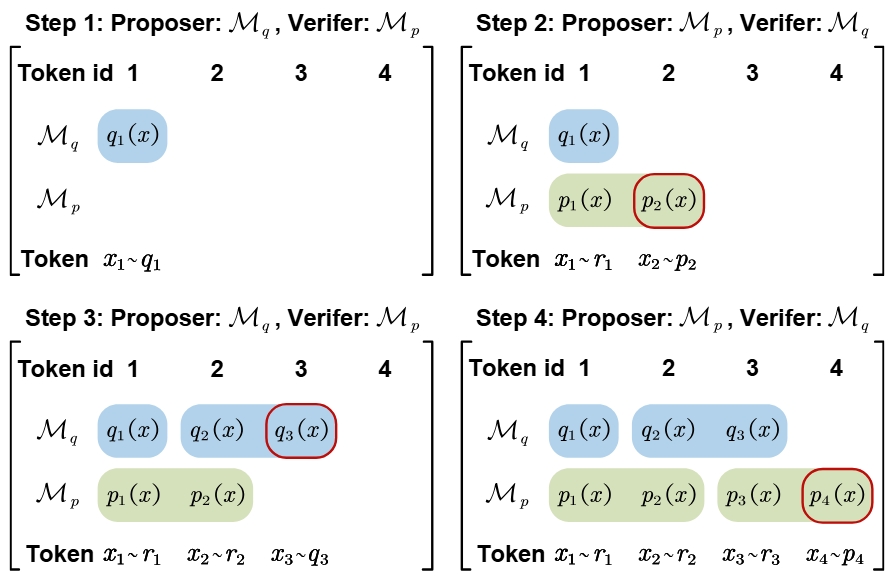
Figure 2. The sketch of Alternate Proposal Framework. A continuous colored block indicates a single model invocation, with the bonus token highlighted in a red rounded box. Beginning from Step 2, \(\mathcal{M}_q\) and \(\mathcal{M}_p\) are invoked alternately. Each invocation involves both the verification of the current token and the generation of a bonus token. For clarity, we assume that the proposal length for each model is 1 and that all proposed tokens are accepted.
In standard SD, the proposer and verifier are fixed, with one model consistently serving as the proposer and the other as the verifier, which fails to fully leverage the bonus token. In SD, when all tokens from the proposal model are accepted by the target model, the target model will naturally generate an additional token, referred to as the bonus token. However, since the bonus token is drawn from the target model’s distribution rather than the ensemble distribution, it cannot be directly appended to the ensemble output. Therefore, we propose an alternative approach: treating the bonus token as a proposal from the target model, which is then verified by the proposer model. This insight leads to the development of a more efficient framework, the Alternate Proposal Framework, illustrated in Figure 2:
- \( \mathcal{M}_q \) proposes \( \gamma_q \) tokens verified by \( \mathcal{M}_p \).
- If all tokens are accepted, \( \mathcal{M}_p \) generates a bonus token treated as \( \mathcal{M}_p \)’s proposal.
- \( \mathcal{M}_q \) verifies this bonus token, creating a feedback loop.
3.2 Generalization to \( n \)-Model Ensembles
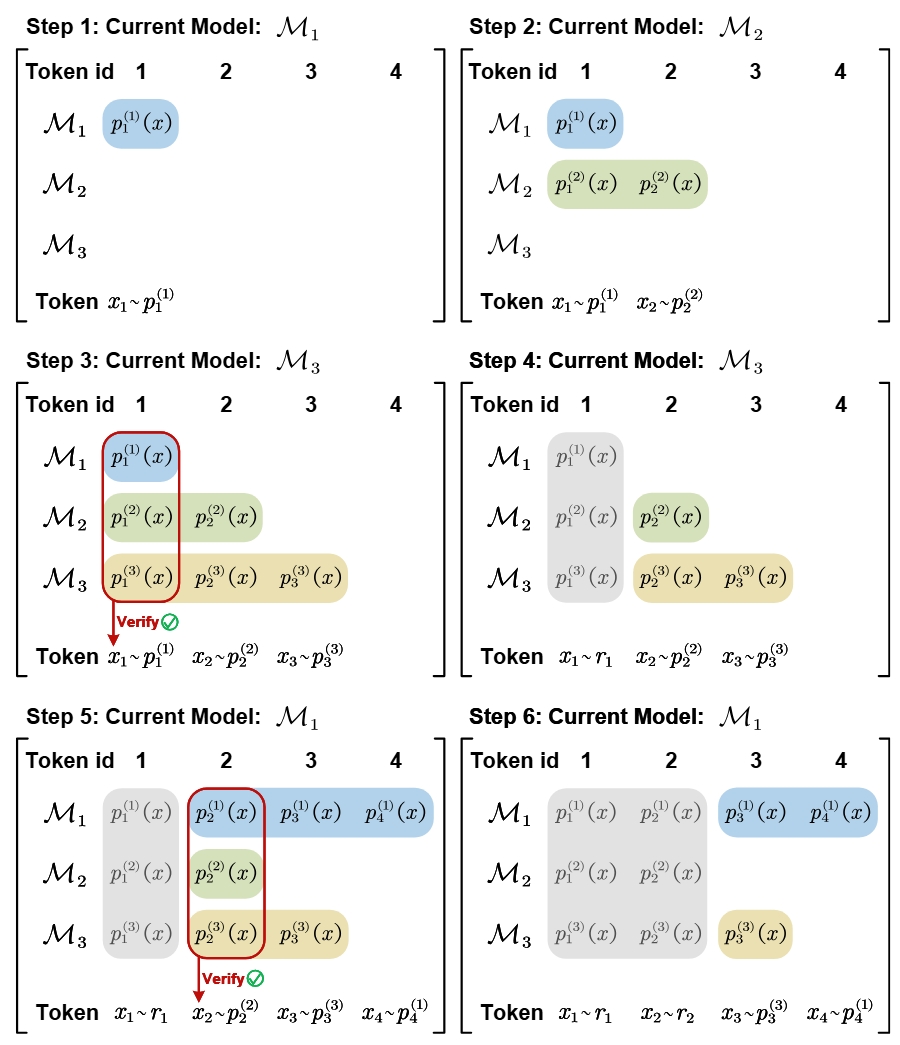
Figure 3. The sketch of SE in three-model ensemble scenario. The colored boxes represent the stored probability distributions, while the grey boxes represent the discarded ones. Each invocation involves scoring the current proposal tokens and generating a bonus token. For clarity, we assume that the proposal length for each model is 1 and that all proposed tokens are accepted.
In this subsection, we extend SE to the \(n\)-model ensemble scenario. The core principles remain similar to the two-model case, with acceleration driven by two key factors. First, each model can score the proposals of other models in parallel, where scoring refers to computing the probability distribution of a proposal from other models. Second, during scoring, a model can naturally generate a bonus token, which further improves efficiency.
As shown in Figure 3, the process begins in step 1 with the default proposal model, \(\mathcal{M}_1\), generating a proposal token \(x_1\). In step 2, \(\mathcal{M}_2\) scores \(x_1\) while simultaneously generating a bonus token \(x_2\). Similarly, in step 3, \(\mathcal{M}_3\) scores both \(x_1\) and \(x_2\) in parallel and produces another bonus token, \(x_3\). At this point, \(x_1\) has been scored by both \(\mathcal{M}_2\) and \(\mathcal{M}_3\), enabling the computation of its ensemble distribution \(r_1(x)\) for verification. The associated distributions \(p_1^{(1)}(x)\), \(p_2^{(1)}(x)\), \(p_3^{(1)}(x)\) are no longer needed and are discarded.
If \(x_1\) is accepted, \(\mathcal{M}_1\) computes \(p_2^{(1)}(x)\), \(p_3^{(1)}(x)\), \(p_4^{(1)}(x)\) in parallel as shown in step 5, allowing verification of \(x_2\). Otherwise, if \(x_1\) is rejected, all stored distributions are cleared, and \(\mathcal{M}_1\) generates a new proposal, similar to step 1.
Experiments show 1.27×–1.85× speedups for 3-model ensembles on code generation tasks.
4. Experimental Results
4.1 Experimental Configuration
We test SE across multiple tasks including code generation, mathematical reasoning, multi-task understanding, and text summarization on HumanEval, GSM8K, MMLU and CNNDM, respectively.
Two ensemble functions were tested:
- Weighted Ensemble (WE):
\[ r(x) = \lambda q(x) + (1-\lambda)p(x) \]- Two-model: \(\lambda = 0.5\), \(T = 1\)
- Three-model: Equal weights (\(1/3\))
- Contrastive Decoding (CD):
\[ r(x) = \text{Softmax}(l_p - \mu l_q) \]- \(\mu = 0.1\), \(T \in \{0, 1\}\)
Among two ensemble functions, three methods are compared: (1) the standard ensemble (WE, CD); (2) an accelerated version with speculative decoding (SD), using the smallest model as the proposal and the ensemble model as the target (WE-SD, CD-SD); and (3) Speculative Ensemble (WE-SE, CD-SE).
We experiment on different types of LLMs, shown as below.
| Ensemble Type | Model Pair | Proposer (\(\mathcal{M}_q\)) | Verifier (\(\mathcal{M}_p\)) |
|---|---|---|---|
| WE | Llama-Vicuna | Llama-2-7B | Vicuna-7B-V1.5 |
| Qwen-3b | Qwen2.5-3B-Instruct | Qwen2.5-Coder-3B-Instruct | |
| Qwen-1.5b | Qwen2.5-1.5B-Instruct | Qwen2.5-Coder-1.5B-Instruct | |
| CD | Llama-3 | Llama-3.2-1B | Llama-3.1-8B-Instruct |
| Llama-2 | Llama-68M | Llama-2-7B | |
| OPT | OPT-125M | OPT-13B |
4.2 Main Results
Weighted Ensemble (WE) Performance
| Model Configuration | Method | Speedup Factor | |||
|---|---|---|---|---|---|
| HumanEval | GSM8K | MMLU | CNNDM | ||
| Llama-Vicuna | WE | 1.00× | 1.00× | 1.00× | 1.00× |
| WE-SD | 1.27× | 1.21× | 1.19× | 1.15× | |
| WE-SE | 1.58× | 1.52× | 1.41× | 1.46× | |
| Qwen-3b | WE | 1.00× | 1.00× | 1.00× | 1.00× |
| WE-SD | 1.13× | 1.06× | 1.09× | 1.08× | |
| WE-SE | 1.62× | 1.52× | 1.42× | 1.38× | |
Contrastive Decoding (CD) Performance
| Model | Temp. (\(T\)) | Method | Speedup Factor | |||
|---|---|---|---|---|---|---|
| HumanEval | GSM8K | MMLU | CNNDM | |||
| Llama-3 | 0 | CD | 1.00× | 1.00× | 1.00× | 1.00× |
| CD-SD | 2.04× | 1.81× | 1.52× | 1.58× | ||
| CD-SE | 2.23× | 2.00× | 1.77× | 1.61× | ||
| 1 | CD | 1.00× | 1.00× | 1.00× | 1.00× | |
| CD-SD | 1.55× | 1.21× | 1.20× | 1.07× | ||
| CD-SE | 1.65× | 1.44× | 1.31× | 1.18× | ||
Recommended citation: Fu J, Jiang Y, Chen J, et al. Speculative Ensemble: Fast Large Language Model Ensemble via Speculation[J]. arXiv preprint arXiv:2502.01662, 2025.
Download Paper
