Fast Large Language Model Collaborative Decoding via Speculation
Published in ICML, 2025
1. Introduction: The Need for Efficient Collaborative Inference
Collaborative decoding for Large Language Models (LLMs) enhances output quality by combining outputs from multiple models at each generation step. However, this approach incurs significant computational overhead, as standard collaborative methods require each model to perform a forward pass for every token, leading to a total cost of \(O(nT)\) for \(n\) models and \(T\) tokens.
We propose Collaborative Decoding via Speculation (CoS), a novel framework that accelerates collaborative decoding by leveraging speculative decoding principles. CoS achieves 1.11×–2.23× speedups across diverse settings without compromising generation quality. Its core innovations are: (1) sampling from a combined distribution of models rather than a single model, and (2) an alternate proposal framework that utilizes bonus tokens efficiently by alternating proposer and verifier roles.
2. Background: Speculative Decoding and Its Extension
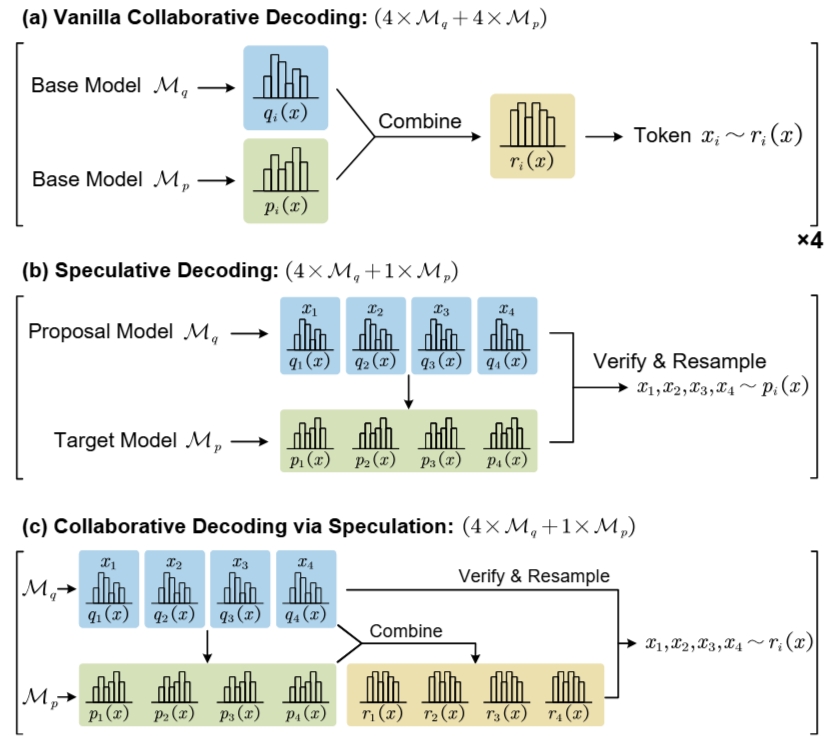
Figure 1. (a) Vanilla collaborative decoding, (b) speculative decoding, (c) CoS (Naive-CoS variant).
2.1 Limitations of Vanilla Collaborative Decoding
Standard collaborative decoding computes the token distribution using functions like weighted averaging or contrastive subtraction:
\[ r_i(x) = \sum_{k=1}^n \lambda_k p_i^{(k)}(x) \] This requires \(n\) forward passes per token, causing high latency as shown in Figure 1(a).
2.2 Speculative Decoding Revisited
Speculative Decoding (SD) accelerates generation using:
- A proposal model \( \mathcal{M}_q \) to generate candidate tokens.
- A verifier model \( \mathcal{M}_p \) to verify them in parallel.
Given \( \gamma \) proposal tokens \( x_{i+1}, \ldots, x_{i+\gamma} \), verification is based on: \[ u_j \leq \min\left(1, \frac{p_{i+j}(x)}{q_{i+j}(x)}\right) \] Rejected tokens are resampled from a renormalized residual distribution.
3. Collaborative Decoding via Speculation (CoS)
3.1 Naive-CoS: Speculative Decoding with Combined Distribution
Naive-CoS extends SD by verifying tokens using a combined distribution \(r(x)\):
- For weighted ensemble (WE):
\[ r(x) = \lambda q(x) + (1-\lambda) p(x) \] - For contrastive decoding (CD):
\[ r(x) = \text{Softmax}(l_p - \mu l_q) \] Verification becomes: \[ u_j \leq \min\left(1, \frac{r_{i+j}(x)}{q_{i+j}(x)}\right) \] This ensures generated tokens align with \(r(x)\), forming the foundation of CoS.
3.2 Alternate Proposal Framework
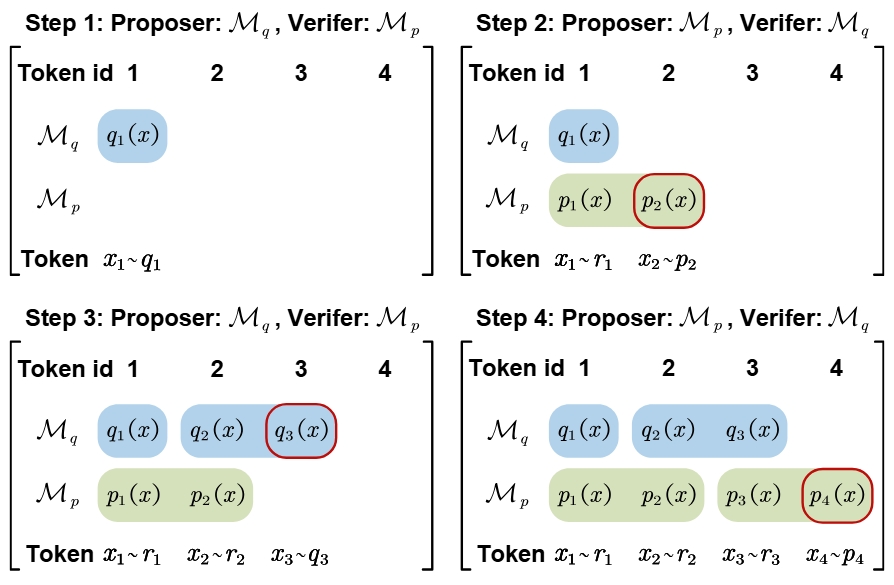
Figure 2. Alternate Proposal Framework alternating proposer/verifier roles to utilize bonus tokens.
When all proposed tokens are accepted, the verifier emits a bonus token. CoS treats this bonus as the next proposal, enabling the models to alternate proposer/verifier roles:
- \( \mathcal{M}_q \) proposes \( \gamma_q \) tokens → verified by \( \mathcal{M}_p \)
- If accepted, \( \mathcal{M}_p \) emits a bonus token → verified by \( \mathcal{M}_q \)
This feedback loop improves utilization and throughput.
3.3 Generalization to \(n\)-Model Collaboration
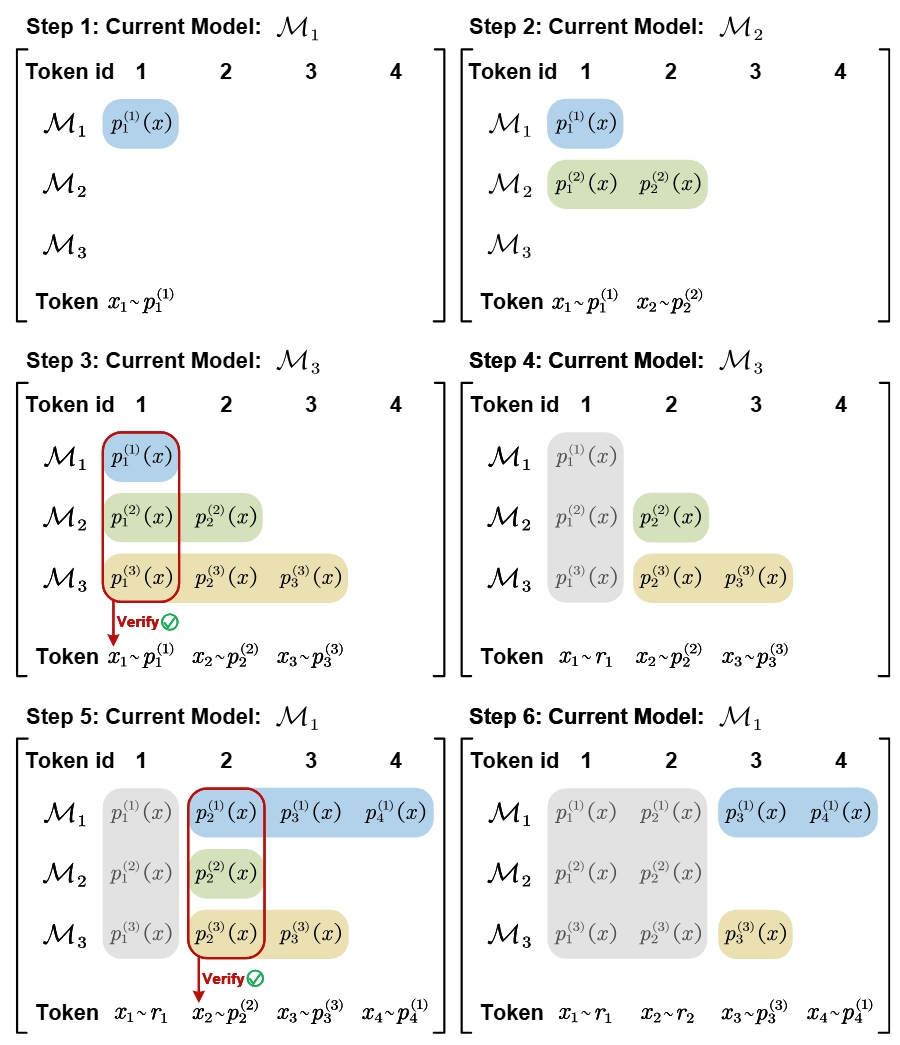
Figure 3. CoS applied to three-model setting with scoring and bonus token chaining.
In the \(n\)-model CoS:
- Each model scores proposals from others in parallel.
- Each scoring pass also emits a bonus token.
- Verification of a token happens only after being scored by all other models.
This extension preserves the theoretical efficiency guarantees.
4. Experimental Results
4.1 Experimental Configuration
We evaluate CoS on four benchmarks: HumanEval, GSM8K, MMLU, and CNNDM, across weighted ensemble and contrastive decoding.
Model Pairs:
| Name | M_q | M_p |
|---|---|---|
| Weight Ensemble (WE) | Llama-Vicuna | Llama-2-7B, Vicuna-7B-V1.5 |
| Qwen-3b | Qwen2.5-3B-Instruct, Qwen2.5-Coder-3B-Instruct | |
| Qwen-1.5b | Qwen2.5-1.5B-Instruct, Qwen2.5-Coder-1.5B-Instruct | |
| Contrastive Decoding (CD) | Llama-3 | Llama-3.2-1B, Llama-3.1-8B-Instruct |
| Llama-2 | Llama-68M, Llama-2-7B | |
| OPT | OPT-125M, OPT-13B |
Compared Methods:
We compare the following decoding strategies:
- Ensemble Decoding (WE, CD) – standard ensemble with weighted or contrastive decoding.
- Parallel Ensemble Decoding (WE-P, CD-P) – parallel processing version of standard ensemble methods, where each model computes its distribution independently and in parallel.
- Speculative Decoding (WE-SD, CD-SD) – acceleration using the smallest model as proposer and the ensemble distribution as verifier.
- Collaborative Decoding via Speculation (WE-CoS, CD-CoS) – our proposed method using alternating roles and speculative ensemble sampling.
4.2 Main Results
Weighted Ensemble (WE) Performance
| Model | Method | HumanEval | GSM8K | MMLU | CNNDM |
|---|---|---|---|---|---|
| Llama-Vicuna | WE | 1.00x | 1.00x | 1.00x | 1.00x |
| WE-P | 0.69x | 0.73x | 0.70x | 0.75x | |
| SD | 1.27x | 1.21x | 1.19x | 1.15x | |
| CoS | 1.58x | 1.52x | 1.41x | 1.46x | |
| Qwen-3b | WE | 1.00x | 1.00x | 1.00x | 1.00x |
| WE-P | 0.74x | 0.79x | 0.79x | 0.77x | |
| SD | 1.13x | 1.06x | 1.09x | 1.08x | |
| CoS | 1.62x | 1.52x | 1.42x | 1.38x | |
| Qwen-1.5b | WE | 1.00x | 1.00x | 1.00x | 1.00x |
| WE-P | 0.63x | 0.62x | 0.64x | 0.63x | |
| SD | 1.11x | 1.13x | 1.08x | 1.10x | |
| CoS | 1.56x | 1.46x | 1.34x | 1.35x | |
| Qwen-1.5b (3 Model) | WE | 1.00x | 1.00x | 1.00x | 1.00x |
| WE-P | 0.54x | 0.73x | 0.80x | 0.82x | |
| SD | 0.96x | 0.92x | 0.98x | 0.95x | |
| CoS | 1.85x | 1.53x | 1.38x | 1.27x |
Contrastive Decoding (CD) Performance
| Model | T | Method | HumanEval | GSM8K | MMLU | CNNDM |
|---|---|---|---|---|---|---|
| Llama-3 | 0 | CD | 1.00x | 1.00x | 1.00x | 1.00x |
| CD-P | 0.41x | 0.40x | 0.41x | 0.41x | ||
| SD | 2.04x | 1.81x | 1.52x | 1.58x | ||
| CoS | 2.23x | 2.00x | 1.77x | 1.61x | ||
| 1 | CD | 1.00x | 1.00x | 1.00x | 1.00x | |
| CD-P | 0.39x | 0.41x | 0.42x | 0.41x | ||
| SD | 1.55x | 1.21x | 1.20x | 1.07x | ||
| CoS | 1.65x | 1.44x | 1.31x | 1.18x | ||
| Llama-2 | 0 | CD | 1.00x | 1.00x | 1.00x | 1.00x |
| CD-P | 0.59x | 0.50x | 0.54x | 0.48x | ||
| SD | 1.15x | 1.62x | 1.08x | 0.93x | ||
| CoS | 1.26x | 1.65x | 1.68x | 1.30x | ||
| 1 | CD | 1.00x | 1.00x | 1.00x | 1.00x | |
| CD-P | 0.56x | 0.51x | 0.53x | 0.49x | ||
| SD | 0.94x | 1.16x | 1.23x | 1.10x | ||
| CoS | 1.15x | 1.20x | 1.37x | 1.11x |
Recommended citation: Fu J, Jiang Y, Chen J, et al. Fast Large Language Model Collaborative Decoding via Speculation[J]. arXiv preprint arXiv:2502.01662, 2025.
Download Paper
