Mimic In-Context Learning in Multimodal Tasks
Published in CVPR, 2025
1. Introduction: Toward Efficient and Stable Multimodal ICL
While In-Context Learning (ICL) empowers Large Multimodal Models (LMMs) to generalize without fine-tuning, its performance is highly sensitive to in-context demonstration (ICD) configurations and incurs considerable computational costs, especially under long image-text contexts.
We propose MimIC, a novel framework that mimics the shift effect of ICL by inserting lightweight, query-dependent shift vectors into attention heads. Unlike standard ICL, MimIC eliminates the need for ICD configuration at inference time, offering robust performance with fewer training samples and lower latency. Experiments show that MimIC matches or surpasses 32-shot ICL across VQA, OK-VQA, and captioning tasks, while reducing hallucinations and outperforming prior shift-based methods.
2. Mechanism Behind ICL: a Shift Vector View
Numerous studies have sought to explain the underlying mechanisms of In-Context Learning (ICL) from various perspectives. Some interpret ICL as a form of implicit Bayesian inference, while others decompose it into task identification and task learning. In this work, we adopt a shift vector perspective. Under this framework, In-Context Demonstrations (ICDs) are viewed as inducing a shift in the representation of the original query, as illustrated in Figure 1(a).
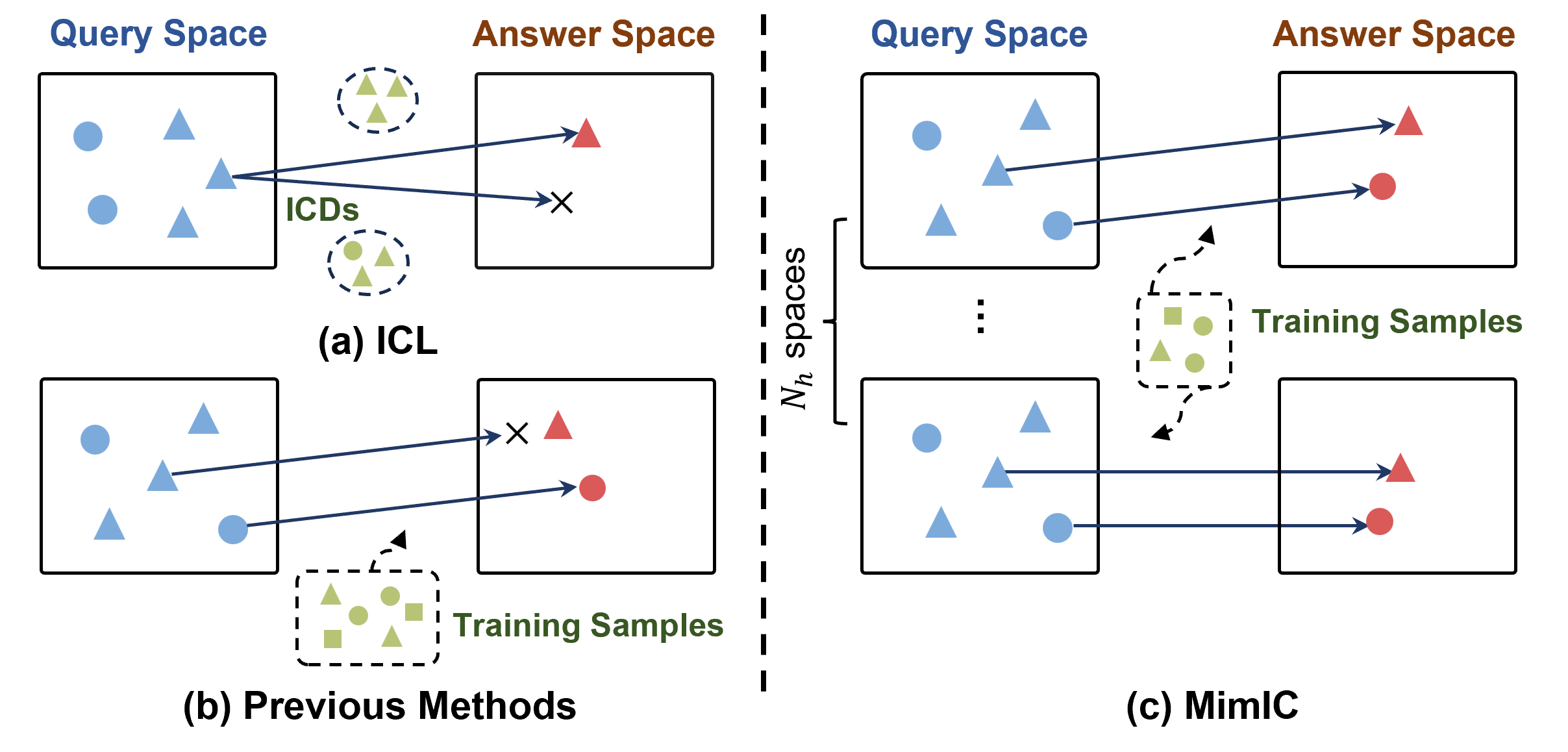
Figure 1. Sketches of shift effects from query space to answer space. (a) Traditional ICL induces the shift vector by ICDs, which is sensitive to ICD configurations, i.e., changing one ICD make prediction incorrect. (b) Previous shift vector-based methods insert a query-independent shift vector learned from a large training set, causing equal shift magnitude for diverse queries, which may make prediction incorrect. (c) MimIC assigns a unique query-dependent shift vector learned from fewer training samples after each attention head layer, shifting diverse magnitude for different queries, thus achieving stronger generalization ability.
However, this shift is inherently unstable, as variations in the order or selection of ICDs can lead to substantial differences in model performance. To address this issue, prior work has proposed heuristic approaches to estimate a shift vector, which is then applied to certain layers of the model to emulate the effect of ICDs. As illustrated in Figure 1(b), these methods remain fixed during inference—that is, the same precomputed shift is applied to all queries—which limits their ability to adapt to complex and diverse task settings. In this work, we build upon the mathematical formulation of the shift vector view to propose a more principled and precise approach to shift simulation. As shown in Figure 1(c), our method accounts for variations across different attention heads, enabling the model to capture information in multiple subspaces. Furthermore, it dynamically adjusts the magnitude of the shift based on the input query, introducing adaptability. Extensive experiments validate the effectiveness of our proposed method.
3. Mimicking In-Context Learning
3.1 Mathematic Analyses
In this section, we provide a mathematical explanation for why ICDs can be interpreted as a shift vector applied to the query.
ICL allows large language models (LLMs) or large multimodal models (LMMs) to generalize to new tasks by providing a few ICDs directly in the input. Formally, the prompt context is defined as \( C = \{ X_D, X \} \), where \( X_D = \{X_1, X_2, \dots, X_k\} \in \mathbb{R}^{l_D \times d} \) represents the concatenation of \( k \) ICDs, and \( X \in \mathbb{R}^{l_q \times d} \) is the query input. Here, \( l_D \) and \( l_q \) denote the number of tokens in \( X_D \) and \( X \), respectively, and \( d \) is the embedding dimension.
Multi-head self-attention applies the self-attention (SA) mechanism over \( N_h \) heads, each parameterized by weight matrices \( W_k, W_q, W_v \in \mathbb{R}^{d \times d_h} \) to project \( C \) into keys \( K_C \), queries \( Q_C \), and values \( V_C \). Typically, \( d_h \) is set to \( d/N_h \) to reduce parameter usage by operating each attention head in a lower-dimensional space. For a specific head, the key mapping is defined as:
\[K_C = C W_k = \begin{bmatrix} X_D \\ X \end{bmatrix} W_k = \begin{bmatrix} K_D \\ K \end{bmatrix}.\]Similarly, we compute the corresponding \( Q_D, Q \), and \( V_D, V \) using \( W_q \) and \( W_v \), respectively. For each query vector \( q \in Q \), the single-head self-attention operation is:
\[\begin{aligned} & \text{SA} \left(q, \begin{bmatrix} K_D \\ K \end{bmatrix}, \begin{bmatrix} V_D \\ V \end{bmatrix} \right) \\ &= \text{softmax}\left( \begin{bmatrix} q K_D^\top, q K^\top \end{bmatrix} \right) \begin{bmatrix} V_D \\ V \end{bmatrix} \\ &= \left[ \frac{\exp\left(q K_D^\top\right)}{Z_1+Z_2}, \frac{\exp\left(q K^\top\right)}{Z_1+Z_2}\right] \begin{bmatrix} V_D \\ V \end{bmatrix} \\ &= \frac{Z_2}{Z_1+Z_2} \frac{\exp(q K^\top)}{Z_2} V + \frac{Z_1}{Z_1+Z_2} \frac{\exp(q K_D^\top)}{Z_1} V_D \\ &= \frac{Z_2}{Z_1+Z_2} \text{softmax}(q K^\top) V + \frac{Z_1}{Z_1+Z_2} \text{softmax}(q K_D^\top) V_D \\ &= (1 - \mu) \text{SA}(q, K, V) + \mu \text{SA}(q, K_D, V_D) \\ &= \underbrace{\text{SA}(q, K, V)}_{\text{standard attention}} + \underbrace{\mu \left(\text{SA}(q, K_D, V_D) - \text{SA}(q, K, V)\right)}_{\text{shift vector}} \end{aligned}\]where \( \mu \) is a scalar representing the normalized attention weights over the ICDs:
\[ \mu(q, K_D, K) = \frac{Z_1(q, K_D)}{Z_1(q, K_D) + Z_2(q, K)}, \]
where \(Z_1(q, K_D) = \sum_{i=1}^{l_D} \exp(q K_D^\top)_i\) and \(Z_2(q, K) = \sum_{j=1}^{l_q} \exp(q K^\top)_j\).
SA equation shows that the self-attention over the prompt context \( C \) can be decomposed into two terms. The first term, “standard attention”, is the self-attention over the query tokens and is independent of the ICDs. The second term, “shift vector”, represents the effect of ICDs in shifting the query space toward the answer space. This shift effect is computed as the attention between the ICDs and the query \( q \), and is governed by the difference term \( \text{SA}(q, K_D, V_D) - \text{SA}(q, K, V) \) and the scalar \( \mu(q, K_D, K) \), both of which are dependent on the ICDs.
3.2 Mimicking ICD Affected Terms
From equations of \(\mu \) and SA, we observe that only \( SA(q,K_D,V_D) \) and \( Z1(q,K_D) \) are affected by ICDs. Let’s tackle them one by one.

Figure 2. MimIC attention head. MimIC changes the attention mechanism for each head, which inserts a learnable shift vector with a query-dependent magnitude.
To approximate \( Z_1(q, K_D) \), we note that it is a positive scalar dependent solely on the current query token \( q \) and the ICD keys \( K_D \). Therefore, we use a simple mapping: a trainable linear layer \( f(\cdot): \mathbb{R}^{d_h} \to \mathbb{R} \) to approximate \( \log Z_1 \). For the attention difference term, as shown in Figure 2, we insert a learnable vector \( v \in \mathbb{R}^{d_h} \) in each attention head to capture the general shift effect for this head. Then, the output of equation of SA in a MimIC attention head is computed as: \[ \operatorname{SA}(q, K, V) + \tilde{\mu}(q, K) v, \] where \( \tilde{\mu}(q, K) = \tilde{Z_1}(q)/(\tilde{Z_1}(q) + Z_2(q, K)) \) and \( \tilde{Z_1}(q) = \exp(f(q)) \). After obtaining the outputs from all MimIC attention heads, they are concatenated, flattened, and passed through the matrix \( W_o \in \mathbb{R}^{d \times d} \) and a feed-forward network (FFN) layer.
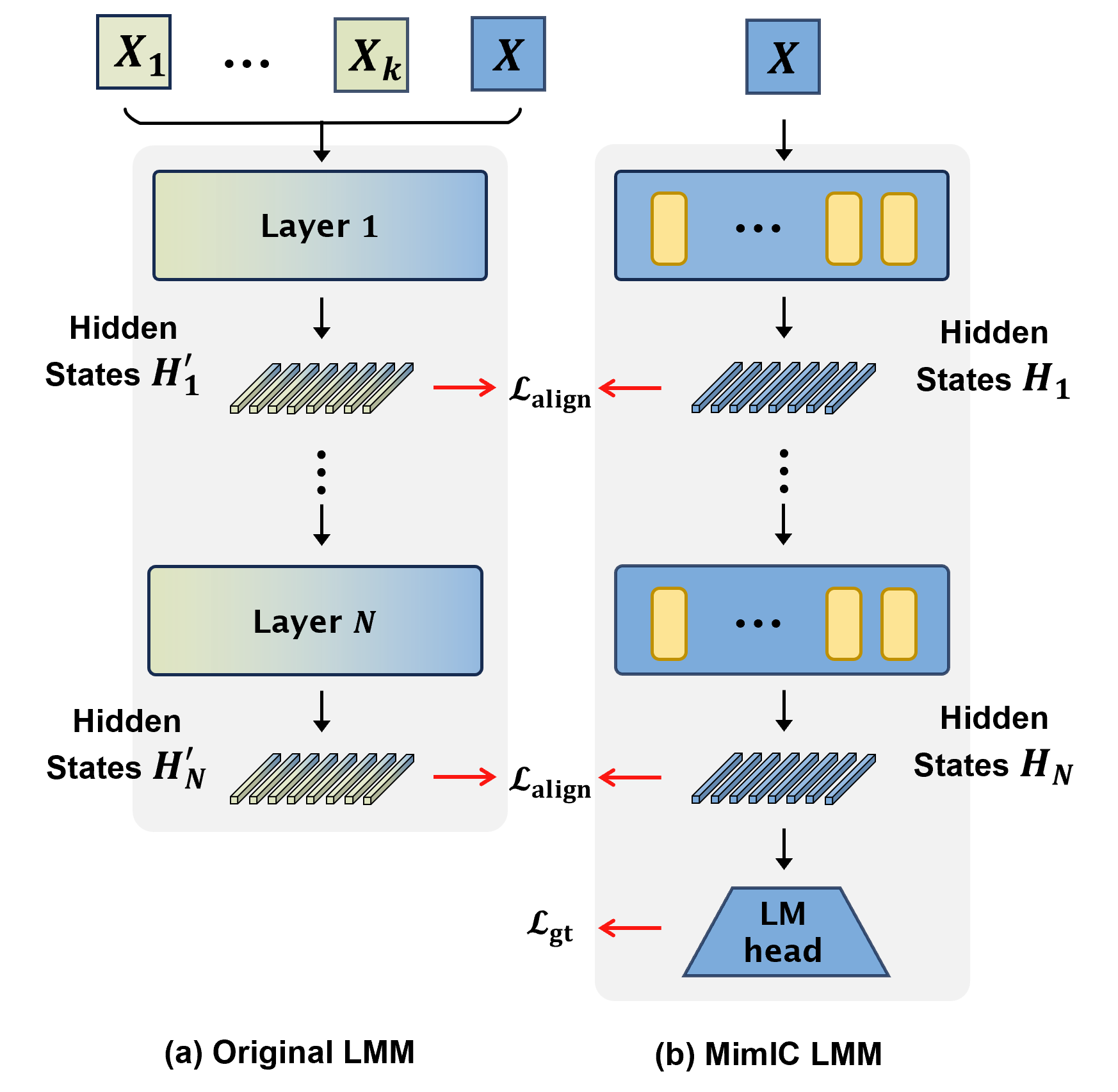
Figure 3. Overall training framework of MimIC. (a) The original LMM processes k ICDs and query input as conventional ICL, generating hidden states H1' to HN' at each layer. (b) In MimIC LMM, only a single query input X is processed, producing shifted hidden states H1 to HN, which are aligned with the original hidden states via the alignment loss L_align. Additionally, the logits of language modeling head is used to compute ground truth loss L_gt. The yellow blocks represent MimIC attention heads.
Given this MimIC attention head, we replace all the self-attention heads of the original LMM to obtain the MimIC LMM as shown in Figure 3(b). Then we hope MimIC LMM can handle a single query \( X \) in the same way the original LMM implements ICL, i.e., using the ICDs \( X_D \) to produce the result for \( X \). To achieve this, given a training set, we randomly select \( k \) samples as ICDs \( X_D \) and one sample as the query \( X \). As shown in Figure 3(a), for the original LMM, we input the context \( C = \{X_D, X\} \) into it to get the hidden states at each layer, which are recorded as \( \mathcal{H}^\prime = \{H_1^\prime, \dots, H_N^\prime\} \). For MimIC LMM, we only input \( X \) into it to get the hidden states \( \mathcal{H} = \{H_1, \dots, H_N\} \). To make MimIC LMM behave similarly to the original LMM, we set an alignment loss \(\mathcal{L}_{\text{align}}\), i.e., layer-wise MSE, to make \( \mathcal{H} \) close to \( \mathcal{H}^\prime \). In addition, we employ the language modeling loss \(\mathcal{L}_{\text{gt}}\) to enhance the model’s performance on downstream tasks,
4. Experimental Results
4.1 Experimental Configuration
We evaluate MimIC on two representative vision-language models (LMMs): Idefics-9b and Idefics2-8b-base, referred to as Idefics1 and Idefics2. Experiments are conducted on three benchmark datasets: VQAv2, OK-VQA, and COCO Caption. Idefics1 adopts a cross-attention architecture, while Idefics2 uses a fully autoregressive design, covering two dominant LMM paradigms. For each dataset, 1,000 samples are randomly selected for training. Evaluation follows existing protocols, using 10,000 validation samples from VQAv2 and full validation splits for OK-VQA and COCO.
Compared Methods
We compare MimIC with the following baseline methods:
- Zero-shot: Direct inference without any in-context demonstration.
- Few-shot ICL: Classical in-context learning using 32-shot (Idefics1) or 8-shot (Idefics2) demonstrations.
- RICES: Retrieval-based in-context example selection using image similarity.
- FV (Function Vector): Injects a compressed representation of task features into the model.
- TV (Task Vector): Similar to FV but derived from a different transformation of ICDs.
- LIVE: Adds learned vectors post-FFN layers; trained under a MimIC-style loss.
- LoRA: Fine-tunes the model via low-rank adaptation on attention weights.
- MimIC: Our proposed method that mimics the shift induced by ICDs, with minimal trainable parameters.
4.2 Main Results
Performance Comparison
| Model | Method | #Params (M) | Benchmarks | ||
|---|---|---|---|---|---|
| VQAv2 | OK-VQA | COCO | |||
| Idefics1 | Zero-shot | - | 29.25 | 30.54 | 63.06 |
| 32-shot ICL | - | 56.18 | 48.48 | 105.89 | |
| RICES | - | 58.07 | 51.11 | 110.64 | |
| FV | - | 30.21 | 31.02 | 74.01 | |
| TV | - | 43.68 | 32.68 | 84.72 | |
| LIVE | 0.13 (×0.5) | 53.71 | 46.05 | 112.76 | |
| LoRA | 25.0 (×96.2) | 55.60 | 47.06 | 97.75 | |
| MimIC | 0.26 (×1.0) | 59.64 | 52.05 | 114.89 | |
| Idefics2 | Zero-shot | - | 55.39 | 43.08 | 40.00 |
| 8-shot ICL | - | 66.20 | 57.68 | 122.51 | |
| RICES | - | 66.44 | 55.73 | 111.44 | |
| FV | - | 36.47 | 34.58 | 75.24 | |
| TV | - | 47.12 | 38.27 | 87.61 | |
| LIVE | 0.13 (×0.5) | 67.60 | 54.86 | 126.04 | |
| LoRA | 17.6 (×67.7) | 66.54 | 55.05 | 116.69 | |
| MimIC | 0.26 (×1.0) | 69.29 | 58.74 | 132.87 | |
Bold numbers denote best results. Underlined numbers denote second-best.
Recommended citation: Jiang Y, Fu J, Hao C, et al. Mimic In-Context Learning for Multimodal Tasks[J]. arXiv preprint arXiv:2504.08851, 2025.
Download Paper
