d2Cache: Accelerating Diffusion-Based LLMs via Dual Adaptive Caching
Published in ICLR, 2026
1. Introduction: Breaking the Efficiency Bottleneck of dLLMs
Diffusion-based Large Language Models (dLLMs) offer a compelling non-autoregressive alternative to standard Transformers, but they suffer from a critical efficiency flaw. Unlike Autoregressive models that rely on causal masking to easily cache past computations, dLLMs utilize bidirectional attention, requiring the model to recompute Key-Value (KV) states for the entire sequence at every denoising step. This computational redundancy creates a severe bottleneck, making inference prohibitively slow as sequence length increases.
To bridge this gap, we introduce d²Cache, a training-free framework designed to accelerate dLLMs without retraining. By employing a dual adaptive selection mechanism, d²Cache dynamically identifies and updates only the most critical tokens at each step while caching the rest, effectively simulating a quasi left-to-right generation process. Our experiments demonstrate that d²Cache not only achieves substantial inference speedups (up to 4.8×) but also consistently improves generation quality by stabilizing the diffusion process against premature errors.
2. Preliminary
2.1 Generation process of dLLMs
Unlike Autoregressive models that generate text token-by-token, Diffusion-based LLMs (dLLMs) model the generation as a reverse denoising process. Starting from pure noised sequence \(x_T\), the model iteratively removes noise to recover the target text \(x_0\). At each step \(t\), the model predicts the clean data estimate \(\hat{x}_0\) based on the current noisy state \(x_t\):
\[x_{t−1} = \text{Denoise}(x_t, \theta)\]However, as shown in Figure 1, this iterative generation process cannot use a standard KV cache, which severely reduces inference throughput.
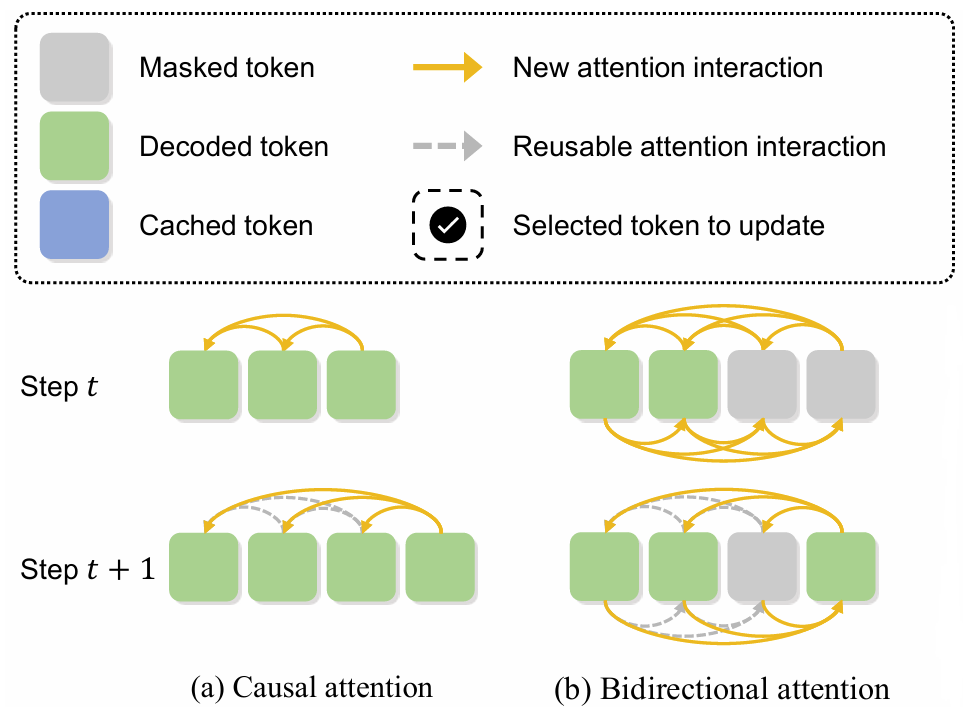
Figure 1. (a) In ARMs, causal attention requires each token to interact only with its preceding tokens. (b) In dLLMs, bidirectional attention requires each token to attend to both its preceding and subsequent tokens, such that any modification in the subsequent tokens necessitates recomputation of the entire sequence.
2.2 Key Observations
Previous methods, such as Fast-dLLM, found significant cosine similarity between KV states in adjacent steps. Therefore, the computational cost of a single forward step could be reduced by periodically refreshing certain sequence segments. To find a more fine-grained refresh strategy, we have the following three observations:
🔍 Observation 1: KV State Dynamics
As shown in Figure 2 (a), the KV states of masked tokens evolve through three phases: (1) a gradual-change phase during the early decoding steps (i.e., steps 0-64), (2) a rapid-change phase in the few steps immediately preceding their decoding (i.e., steps 64-98), and (3) a stable phase after being decoded (i.e., steps 98-255). Notably, it is sufficient to update the KV states of masked tokens only during the rapid-change phase, whereas the KV states of masked tokens can be safely cached for reuse during the gradual-change and stable phases.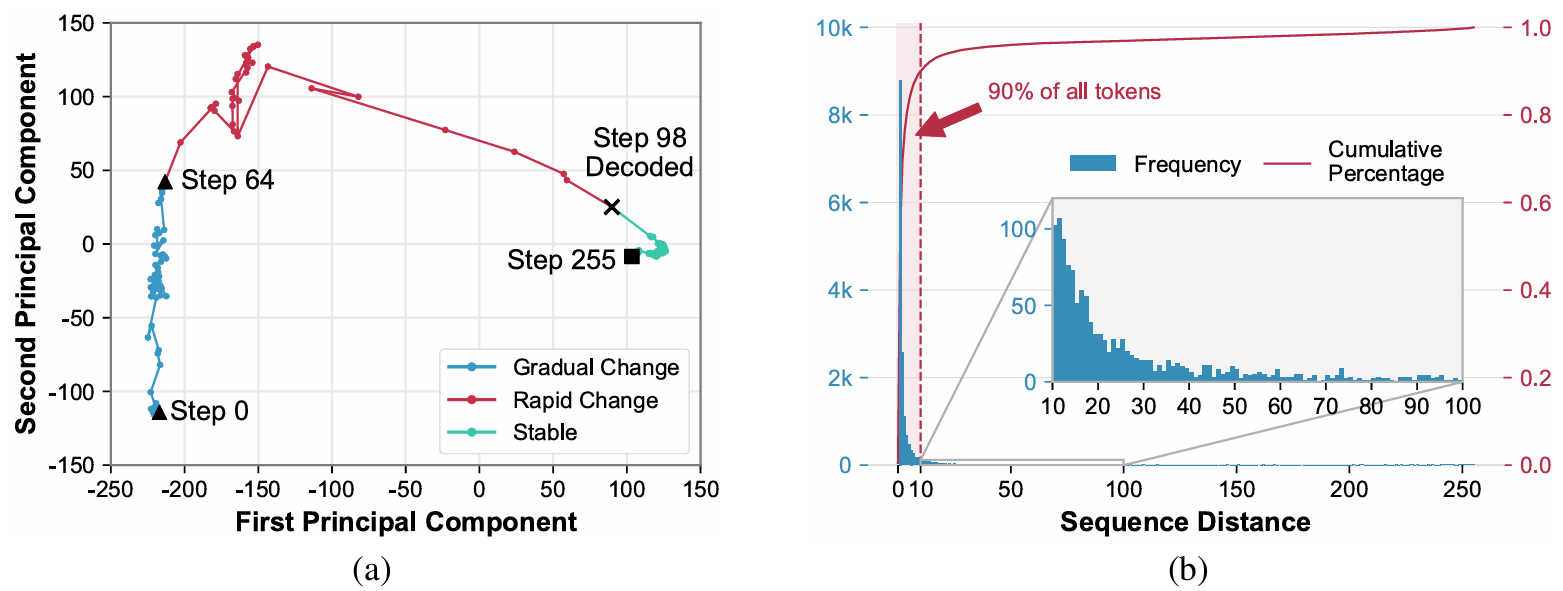
Figure 2. (a) PCA of the trajectory of the 77th masked token on LLaMA-8B-Instruct with GSM8K (sequence length 328, generation length 256, generate in 256 steps). (b) Sequential distances between token pairs decoded in adjacent steps, accumulated from 64 GSM8K samples.
🔍 Observation 2: Decoding Order
As shown in Figure 2 (b), LLaDA-8B-Instruct tends to decode the next masked token from positions close to the most recently decoded token, with 90% of tokens falling within a distance of 10. This indicate that the decoding order of masked tokens correlates with the number of decoded tokens in the local context. Therefore, we can estimate whether the masked token is in the rapid-change phase according to the density of decoded tokens in the local context.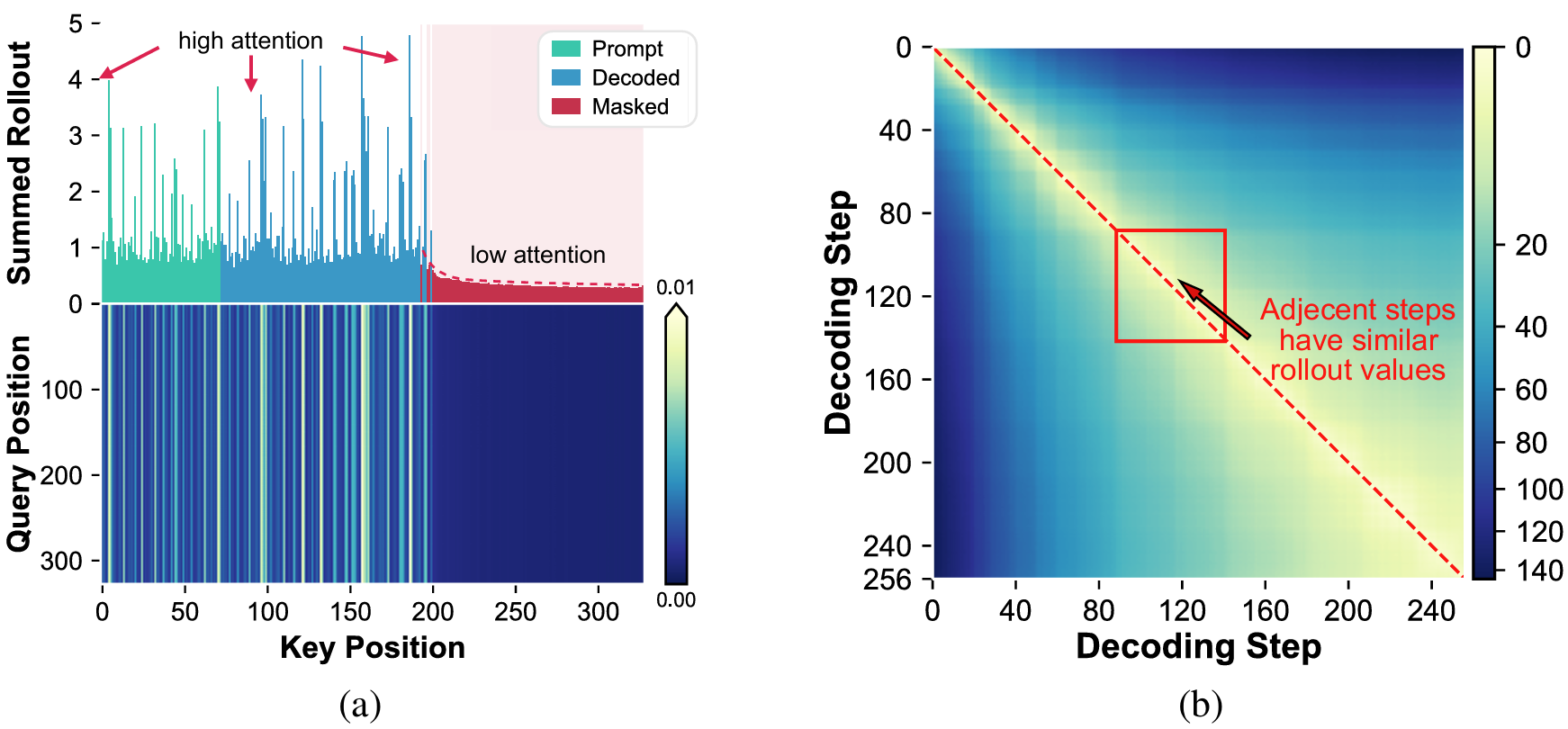
Figure 3. Attention rollout analysis over sequence, where the example and setting are the same as in Figure 2. (a) Attention rollout visualization at step 126, showing the sum of rollout values over all key positions (top) and the pairwise rollout values across different positions (bottom). (b) The total absolute differences in rollout values between each two adjacent decoding steps.
🔍 Observation 3: Attention Patterns
As shown in Figure 3, the attention distribution in dLLMs is highly uneven: prompt and decoded tokens receive most attention from other tokens, while masked tokens only receive negligible attention. Moreover, attention allocations across consecutive decoding steps are highly similar. The attention allocation of the current step can thus be used to select tokens for KV state updates in the next step, i.e., prioritizing tokens that receive greater attention.3. d²Cache: Dual Adaptive Cache
Motivated by the previous observations, we present Dual aDaptive Cache (d²Cache), a training-free approximate KV cache framework for accelerating dLLM inference. To exploit approximate KV cache in dLLMs, d²Cache seeks to adaptively identify tokens whose KV states should be actively updated at each decoding step, while caching the remaining tokens for reuse in a subsequent decoding step.
We first group tokens in dLLMs into three categories: prompt tokens, masked tokens, and decoded tokens. Based on this categorization, we introduce a two-stage fine-grained token selection strategy. ❶ Certainty prior-guided selection from masked tokens. After each forward pass, d²Cache assigns each masked token a score combining prediction confidence and a certainty prior, which represents the density of known tokens (i.e., prompt or decoded ones) in the local context. d²Cache then adaptively selects a subset of masked tokens with higher scores. In light of this, d²Cache naturally enables an alternative decoding scheme guided by the certainty prior rather than prediction confidence alone, yielding higher reliability. ❷ Attention-aware selection from remaining tokens. Furthermore, for the remaining tokens (especially prompt and decoded tokens), d²Cache adaptively selects a subset of tokens with higher attention activations. Finally, for the tokens selected in these two stages, d²Cache updates their KV states at each decoding step, while caching the KV states of the remaining tokens for reuse in a subsequent decoding step.
For formal descriptions, please refer to Section 4 of the original paper.
4. Experimental Results
4.1 Experimental Configuration
We evaluate d²Cache on two representative dLMMs: LLaDA-8B and Dream-v0-7B, referred to as LLaDA-Base/Inst and Dream-Base/Inst. Experiments are conducted on six benchmark datasets: GSM8k, MBPP, Humaneval, Math-500, GPQA and MMLU-Pro. For fair comparisons, we report both inference throughput and latency, where throughput denotes the average number of tokens generated per second and latency denotes the average inference time per sample. All experiments are performed on NVIDIA 3090 24GB GPUs.
Compared Methods
We compare d²Cache with the following baseline methods:
- Vanilla: At each decoding step, the masked position with the highest confidence is replaced with its predicted token.
- dLLM-Cache: The prompt segment and response segment are refreshed at different time intervals, and the cache in the response segment is dynamically refreshed according to changes in V states.
- Fast-dLLM: During semi-autoregressive generation, only the current block and subsequent blocks are recalculated. After each block is generated, the entire sequence is recalculated, and the prompt and completed blocks are cached.
- d²Cache: Our method, which dynamically selects the tokens that need to be updated at the token level at each step.
4.2 Main Results
Performance Comparison
Comprehensive evaluation results on LLaDA-Inst and Dream-Inst.
| Dataset | Method | LLaDA-Inst | Dream-Inst | ||||
|---|---|---|---|---|---|---|---|
| Throughput ↑ | Latency(s) ↓ | Score ↑ | Throughput ↑ | Latency(s) ↓ | Score ↑ | ||
| GSM8K 4-shot Gen. Len. = 256 | Vanilla | 2.77 (1.0×) | 110.26 | 77.6 | 2.62 (1.0×) | 85.94 | 76.7 |
| + dLLM-Cache | 8.29 (3.0×) | 30.34 | 76.8 | 7.50 (2.9×) | 33.75 | 74.6 | |
| + Fast-dLLM | 9.64 (3.5×) | 26.15 | 77.0 | 10.12 (3.9×) | 24.88 | 77.0 | |
| d2Cache | 11.39 (4.1×) | 22.41 | 79.2 | 12.25 (4.7×) | 21.36 | 78.2 | |
| MBPP 3-shot Gen. Len. = 512 | Vanilla | 2.48 (1.0×) | 199.90 | 38.0 | 2.73 (1.0×) | 182.78 | 52.0 |
| + dLLM-Cache | 6.97 (2.8×) | 71.79 | 38.0 | 7.07 (2.6×) | 71.13 | 52.4 | |
| + Fast-dLLM | 6.80 (2.7×) | 73.27 | 38.4 | 7.29 (2.7×) | 69.47 | 52.0 | |
| d2Cache | 11.42 (4.6×) | 43.86 | 39.4 | 12.47 (4.6×) | 40.32 | 58.0 | |
| HumanEval 0-shot Gen. Len. = 512 | Vanilla | 4.99 (1.0×) | 105.76 | 45.1 | 4.39 (1.0×) | 114.86 | 56.7 |
| + dLLM-Cache | 8.67 (1.7×) | 57.48 | 44.5 | 5.35 (1.2×) | 94.33 | 56.5 | |
| + Fast-dLLM | 7.90 (1.6×) | 63.12 | 43.9 | 7.89 (1.8×) | 63.84 | 56.1 | |
| d2Cache | 14.00 (2.8×) | 35.44 | 48.2 | 14.06 (3.2×) | 36.61 | 61.6 | |
| Math-500 4-shot Gen. Len. = 256 | Vanilla | 3.08 (1.0×) | 82.51 | 38.4 | 3.51 (1.0×) | 71.05 | 45.2 |
| + dLLM-Cache | 6.71 (2.2×) | 37.84 | 38.2 | 7.19 (2.0×) | 35.36 | 44.2 | |
| + Fast-dLLM | 10.61 (3.4×) | 23.79 | 38.0 | 10.72 (3.1×) | 23.52 | 44.4 | |
| d2Cache | 12.02 (3.9×) | 20.19 | 38.0 | 13.80 (3.9×) | 18.80 | 44.6 | |
| GPQA 0-shot Gen. Len. = 256 | Vanilla | 6.14 (1.0×) | 43.34 | 25.2 | 6.43 (1.0×) | 41.14 | 30.1 |
| + dLLM-Cache | 11.51 (1.9×) | 22.33 | 27.2 | 10.91 (1.7×) | 23.62 | 31.0 | |
| + Fast-dLLM | 12.41 (2.0×) | 20.66 | 25.7 | 11.75 (1.8×) | 21.79 | 34.6 | |
| d2Cache | 15.04 (2.4×) | 17.08 | 28.4 | 14.65 (2.3×) | 17.52 | 31.5 | |
| MMLU-Pro 5-shot Gen. Len. = 256 | Vanilla | 1.76 (1.0×) | 152.62 | 37.5 | 2.15 (1.0×) | 126.31 | 47.9 |
| + dLLM-Cache | 6.79 (3.9×) | 38.29 | 38.1 | 7.82 (3.6×) | 34.09 | 46.5 | |
| + Fast-dLLM | 8.91 (5.1×) | 29.00 | 37.1 | 9.74 (4.5×) | 27.69 | 45.9 | |
| d2Cache | 9.59 (5.4×) | 27.60 | 33.1 | 10.12 (4.7×) | 25.77 | 46.8 | |
| AVG | Vanilla | 3.54 (1.0×) | 115.73 | 43.6 | 3.64 (1.0×) | 103.68 | 51.4 |
| + dLLM-Cache | 8.16 (2.3×) | 43.01 | 43.8 | 7.64 (2.1×) | 48.71 | 50.9 | |
| + Fast-dLLM | 9.38 (2.7×) | 39.33 | 43.4 | 9.59 (2.6×) | 38.53 | 51.7 | |
| d2Cache | 12.24 (3.5×) | 27.76 | 44.4 | 12.89 (3.5×) | 26.73 | 53.4 | |
Bold numbers denote best results and blue texts denote the speedup ratios.
Recommended citation: Jiang Y, Cai Y, Luo X, et al. d $^ 2$ Cache: Accelerating Diffusion-Based LLMs via Dual Adaptive Caching[J]. arXiv preprint arXiv:2509.23094, 2025.
Download Paper
